- Óptica
- /
- Refração, lentes e inst.
- /
- Refração e Meios Refringentes
A velocidade da luz muda ao passar de um meio para outro
Refração
O fenômeno da refração da luz está associada à mudança de velocidade da luz ao passar de um meio para outro. A velocidade da luz modifica-se na refração, isto é, na passagem de um meio para outro.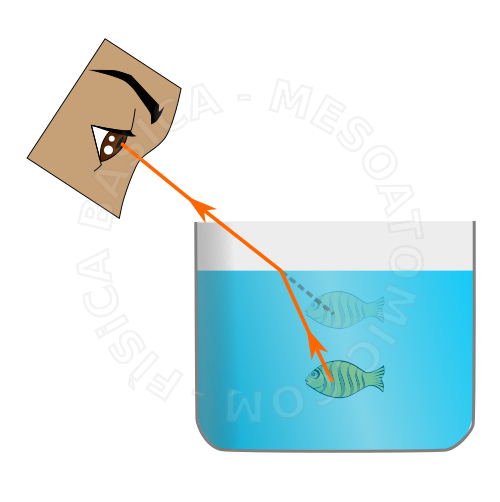
-
Para o estudo da refração, as seguintes definições são importantes:
- Dioptro
- é o conjunto de dois meios refringentes separados por uma superfície. As substâncias que constituem os meios transparentes são denominadas meios refringentes. Quanto maior a refringência de um meio menor a velocidade da luz neste meio.
- A velocidade da luz no vácuo \((c)\)
- é \(300.000 \frac{km}{s}\) ou \(3.10^8 \frac{m}{s}\) . A velocidade da luz no ar é aproximada para o valor da velocidade dela no vácuo.
- O índice de refração absoluto \((n)\)
- é o quociente entre a velocidade da luz no vácuo, \(c\) , e a velocidade da luz no meio em questão:
- \begin{equation} n=\frac{velocidade\ da\ luz\ no\ v\acute{a}cuo}{velocidade\ da\ luz\ no\ meio}\ = \frac{c}{v}. \end{equation} Exemplos de materiais com diferentes índices de refração:
-
Substância \(n\) Água pura 1,33 Sal de cozinha 1,54 Diamante 2,42 Álcool etílico 1,36 Glicerina 1,47 Vidro crown 1,52 Gelo 1,31 Parafina 1,43 - O índice de refração relativo
- de um meio \(A\) em relação a um outro meio \(B\) é obtido através da fórmula: \begin{equation} n_{ab}=\frac{n_{A}}{n_{B}}=\frac{v_{B}}{v_{A}}, \end{equation} onde \(n_A\) é o índice de refração do meio \(A\) e \(n_B\) é o índice de refração do meio \(B\) .
Leis da refração
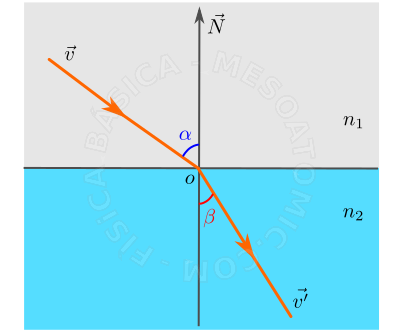
Para um raio de luz incidente na interface de dois meios com índices de refração diferentes, o raio incidente e o refratado não estarão no mesmo plano. Os ângulos, que estes raios fazem com o vetor normal a interface entre os meios, podem ser encontrados com a lei de Snell-Descartes, que diz: Para um raio de luz monocromática passando de um meio para outro, é constante o produto do seno do ângulo, formado pelo raio e a normal, com o índice de refração do meio em que se encontra este raio. Matematicamente, temos \begin{equation} n_{1} sen(\alpha) =n_{2} sen(\beta). \end{equation} Note que quando o raio de luz passa de um meio menos refringente (maior velocidade) para um meio mais refringente (menor velocidade) ele se aproxima da normal, e vice-versa. A figura abaixo ilustra o fenômeno.
Reflexão total
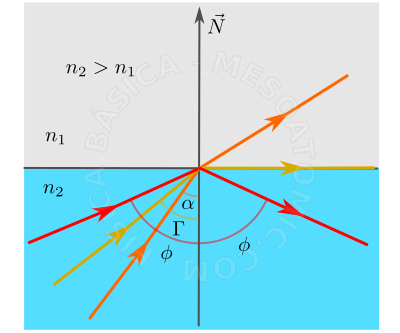
Quando a luz passa de um meio mais refringente para um menos refringente, existe um ângulo limite , tal que para ângulos maiores que este, o raio de luz não consegue mais mudar de meio, de maneira que o raio é totalmente refletido na interface entre os meios. Este fenômeno é importante para aplicações como a fibra óptica e telescópios. O ângulo limite \(\Gamma\) é definido como o ângulo incidente o qual corresponde uma emergência rasante de \(90^{o}\) , quando a luz se propaga do meio mais refringente para o meio menos refringente, isto é \begin{equation} sen(\Gamma)=\frac{n_{1}}{n_{2}}\text{, para }n_{1} \lt n_{2}. \end{equation}
Dioptro plano
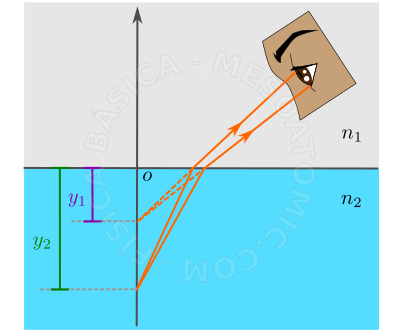
Lâminas de faces paralelas
Quando um raio de luz atravessa uma lâmina de face paralela, ele sai de um meio com um dado índice de refração, digamo \(n_1\) , atravessa um meio com índice \(n_2\) , e volta para o meio de refração \(n_1\) . Usando as leis da refração, encontramos que o raio emergente no meio de refração \(n_2\) será paralelo ao raio incidente neste meio, veja a figura abaixo.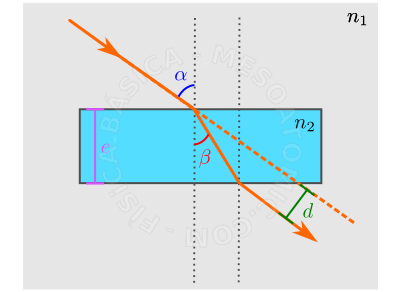
Prisma
O sistema óptico constituído por três meios homogêneos e transparentes separados por duas superfícies planas não paralelas é denominado de prisma.
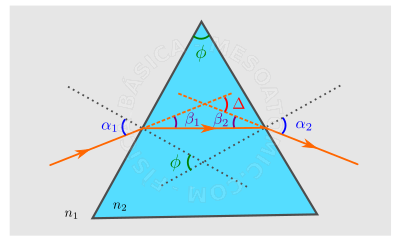
Veja a figura acima. Para este sistema podemos relacionar o ângulo entre as duas faces do prisma, \(\phi\) , com os ângulos com as normais internas \(\beta_1\) e \(\beta_2\) : \begin{equation} \phi = \beta_1 + \beta_2. \end{equation} Também é possível encontrar o ângulo que o raio incidente no prisma fará com o raio que emerge do primas, \(\Delta\) , isto é \begin{equation} \Delta = \alpha_1 + \alpha_2 - \phi, \end{equation} onde \(\alpha_1\) e \(\alpha_2\) são os ângulos que o raio de luz faz com as normais externas ao prisma.
A análise dos prismas ópticos revela-nos que o desvio assume o valor mínimo , \(\Delta_{min}\) , quando o ângulo de incidência na \(1^a\) face e de emergência na \(2^a\) face forem iguais ( \(\alpha_1 = \alpha_2\) ) tal que: \begin{equation} \Delta_{min} = 2 \alpha_{1} - \phi. \end{equation}