- Óptica
- /
- Reflexão e espelhos
- /
- Espelhos Esféricos
Um epelho esférico é uma calota esférica onde ocorre reflexão regular da luz.
Espelhos Esféricos
Tipos de espelhos: 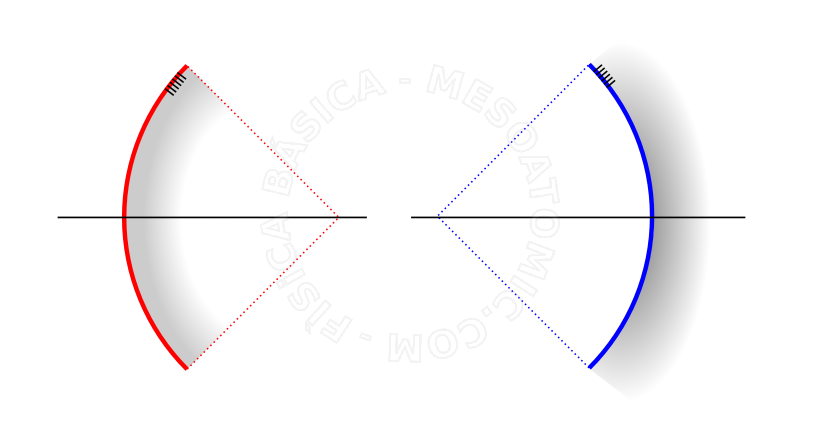
- Espelho esférico côncavo
- Quando a superfície refletora está do lado interno da calota esférica.
- Espelho esférico convexo
- Quando a superfície refletora está do lado externo da calota esférica.
Elementos geométricos

- Centro de curvatura \((C)\)
- é o centro da esfera que contém a calota esférica;
- Raio de curvatura \((r)\)
- é o raio de curvatura da esfera que contém a calota esférica;
- Vértice do espelho \((V)\)
- é o ponto médio da calota esférica;
- Eixo principal \((u)\)
- é a reta que contém o centro \(C\) e o vértice \(V\) do espelho;
- Eixo secundário \((u')\)
- é qualquer reta que contém o centro \(C\) , mas não contém o vértice \(V\) do espelho;
- Foco principal \((F)\)
- é o ponto situado entre o centro de curvatura e o vértice do espelho, para os espelhos esféricos de Gauss . A equação do foco é \(f=\frac{r}{2}\) ;
- Foco Secundário \((F_s)\)
- é o ponto focal que pertence a um eixo secundário e não ao eixo principal. Quando um feixe de raios paralelos incide sobre um espelho esférico paralelamente a um de seus eixos secundários, ele origina um feixe convergente, no caso do espelho côncavo, e divergente, no do convexo. O vértice \(F_s\) de origem do pincel de luz destes raios refletidos situa-se nesse eixo secundário e constitui um dos focos secundários.
Propriedades da reflexão dos raios de luz
Supondo que as trajetórias dos raios de luz formam ângulos pequenos com o eixo óptico (aproximação paraxial), para um espelho esférico temos as seguintes regras para a reflexão:
- Um raio incidente paralelamente ao eixo principal reflete-se em relação ao foco principal.
- Um raio incidente em relação ao foco principal reflete-se paralelamente ao eixo principal.
- Um raio incidente na direção de um eixo do espelho reflete-se sobre si mesmo.
- Um raio incidente no vértice do espelho, e oblíquo a algum eixo, reflete-se simetricamente em relação a este eixo.
- Todo raio de luz que incide num espelho esférico obliquamente ao eixo principal, ao refletir-se, passa pelo respectivo foco secundário.
- Um raio incidente em relação ao foco principal reflete-se paralelamente ao eixo principal.
Imagem produzida por um espelho convexo
Supondo que as trajetórias dos raios de luz de um objeto formam ângulos pequenos com o eixo óptico (aproximação paraxial), nesta situação a imagem de um espelho convexo é sempre: virtual, direita e menor. 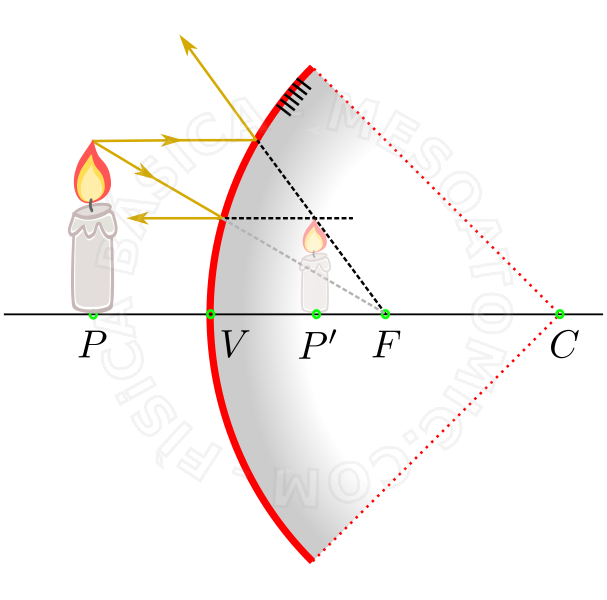
Imagem produzida por um espelho côncavo
Supondo que as trajetórias dos raios de luz de um objeto formam ângulos pequenos com o eixo óptico (aproximação paraxial), é possível encontrar as diferentes imagens que um espelho côncavo pode produzir nesta situação (veja a figura). 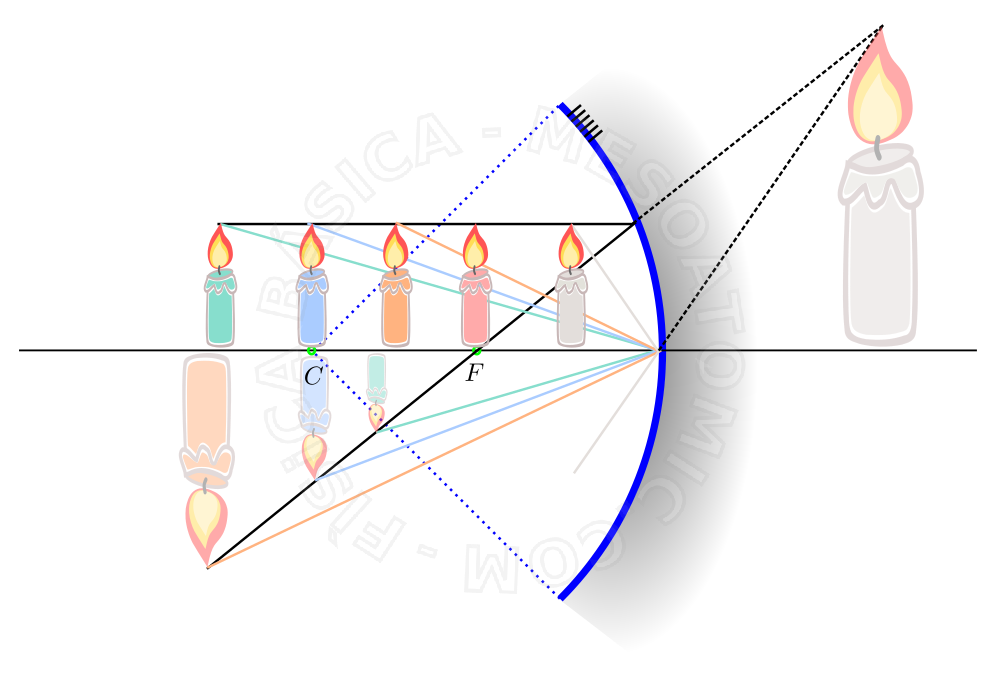
- Vela verde
- é um objeto além do centro de curvatura , cuja imagem é real, invertida e menor .
- Vela azul
- é um objeto sobre o centro de curvatura , cuja imagem é real, invertida e do mesmo tamanho .
- Vela laranja
- é um objeto entre o centro de curvatura e o foco , cuja imagem é real, invertida e maior .
- Vela vermelha
- é um objeto no plano focal , cuja imagem é imprópria (se forma no infinito) .
- Vela cinza
- é um objeto entre o foco e o vértice , cuja imagem é virtual, direita e maior .
Referencial de Gauss
Para realizar o estudo analítico/algébrico dos espelhos esféricos, utilizamos o referencial de Gauss, onde
- O eixo das abscissas
- coincide com o eixo principal do espelho, com origem no vértice e orientado em sentido contrário ao da luz incidente;
- O eixo das ordenadas
- é perpendicular ao eixo principal, com origem no vértice do espelho. O eixo das ordenadas é orientado de maneira que a ordenada \(o\) do objeto seja positiva.
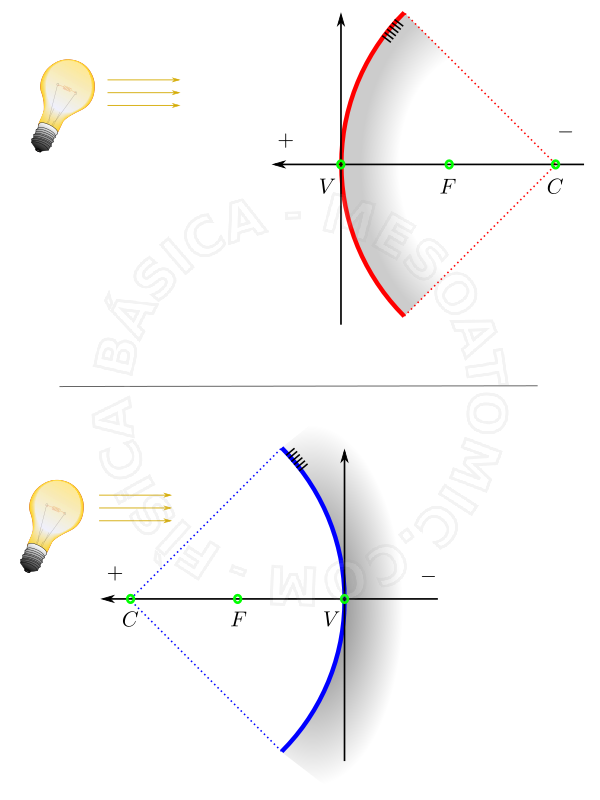
Ilustração do referencial de gaus para o espelho convexo (vermelho) e côncavo (azul).
Equação do aumento linear transversal:
A amplificação \(A\) , ou aumento linear, de uma imagem em um espelho esférico é dada por \begin{equation} A=\frac{i}{o}=\frac{-p'}{p}\ \end{equation} onde \(p\) é a distância do objeto ao vértice do espelho, \(p'\) a distância da imagem ao vértice do espelho, \(o\) o tamanho do objeto, \(i\) tamanho da imagem. Note que: para uma imagem direita, temos \(A\gt0\) , para uma imagem invertida, temos \(A\lt0\) .
Equação de Gauss (pontos conjugados).
A imagem de um objeto, colocado a uma distância \(p\) de um espelho de distância focal \(f\) , forma-se a uma distância \(p’\) do espelho, tal que: \begin{equation} \frac{1}{f}=\frac{1}{p}+\frac{1}{p'}, \end{equation} onde \(p\) é positivo para objetos reais e negativo para objetos virtuais, \(f\) é positivo para o espelho côncavo e negativo para o convexo e \(p’\) é positivo para uma imagem real e negativo para uma imagem virtual. Esta equação também só é valida para aproximação paraxial, isto é, para raios de luz que formam ângulos pequenos com o eixo principal do espelho.
Observações
- As grandezas \(f\) , \(p\) , \(p’\) , \(i\) , \(o\) e \(A\) são algébricas, isto é, elas devem ser introduzidas nas equações com seus respectivos sinais (positivo ou negativo), para que possam produzir resultados corretos.
- Às vezes sistemas ópticos usam dois (ou mais) espelhos, e a imagem formada pelo primeiro espelho serve como objeto para o segundo espelho. Em algumas situações, tal objeto fica situado atrás do segundo espelho. Neste caso, a distância do objeto é negativa, e diz-se que o objeto é virtual.