- Mecânica
- /
- Dinâmica
- /
- Forças Elásticas
Na natureza é possível encontrar diferentes tipos de materiais, com diferentes propriedades. Abordaremos aqui as propriedades elásticas dos materiais, que é a tendência a voltar para o seu estado inicial(equilíbrio) quando deformadas. Exemplos de objetos com tais propriedades são: molas, elásticos, vara de pescar, arco e flecha, e muitos outros.
Forças elásticas
As forças elásticas \(\vec{F}_e\) tem as seguintes características:
- Direção
- Quando um corpo é deformado por uma força, surge uma força elástica na mesma direção desta força.
- Sentido
- A força elástica tem sempre o sentido que tenderá retornar o corpo para o seu estado inicial, posição de equilíbrio.
- Módulo
- O módulo da força elástica depende do tipo de material e do tamanho da deformação, para pequenas deformações (dentro do limite elástico do material em questão) é possível aplicar a Lei de Hooke, veja abaixo.
Lei de Hooke
Para os materiais elásticos dos quais as molas são compostas, dentro do limite elástico, é possível considerar que a intensidade da força restauradora da mola é proporcional à deformação feita nesta. Matematicamente isto é: $$ F_e = - k \Delta x, $$ onde \(k\) é a constante elástica da mola, que é diferente para diferentes materiais, e \(\Delta x = (x - x')\) é a deformação sofrida pela mola em relação a posição natural da mola, \(x`\) . A figura abaixo ilustra o fenômeno. 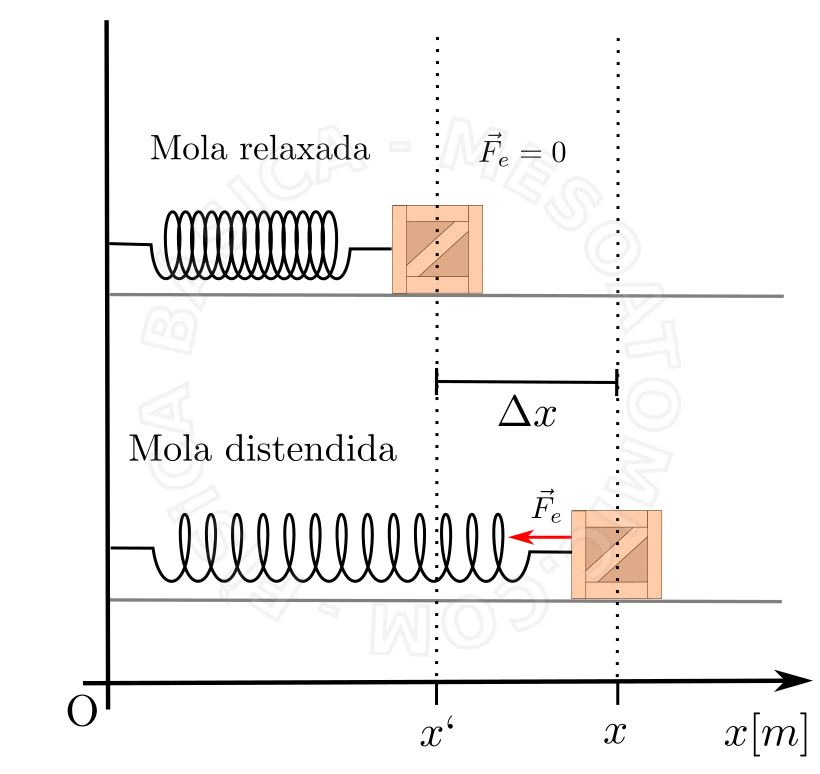
- A constante elástica da mola \(k\) é uma medida de sua "dureza", isto é, quanto maior o valor de \(k\) mais força temos que aplicar para produzir uma deformação.
- A força não depende do comprimento físico \(L\) da mola, mas, em vez disso, depende da deformação \((x` - x\) ) da extremidade livre da mola.
- Por vezes é possível consideramos molas como sendo ideais, isto é, podemos desprezar a massa das molas em comparação a massa dos objetos presos a elas, e que elas sempre retornarão ao seu estado inicial sem deformação permanente.