- Mecânica
- /
- Dinâmica
- /
- Forças
A força é um agente capaz de produzir aceleração e/ou deformação de um corpo.
A unidade de força no SI é o Newton, \([F] = N\) .
Dinâmica é a parte da mecância que estuda as forças e seus efeitos sobre o movimento. Lembre-se que a cinemática só estuda o movimento sem se preocupar com as forças.
Os Diferentes Tipos de Forças
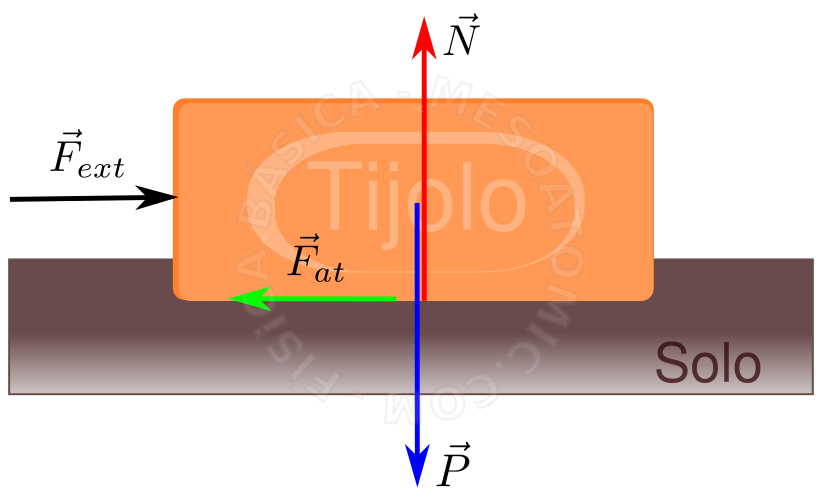
As forças típicas que aparecem em problemas de mecânica podem ser entendidas da seguinte maneira:
- Força resultante \((\vec{F}_r)\)
- Quando várias forças atuam simultaneamente em uma partícula, elas podem ser substituídas por uma única força, que sozinha, terá o mesmo efeito que todas as outras juntas. De forma matemática, escreve-se: \begin{align} \vec{F}_r &= \sum_i^n \vec{F}_i = \\ &= \vec{F}_1+ \vec{F}_2+...+\vec{F}_j+...+\vec{F}_n \end{align}
- Força Peso \((\vec{P})\)
- É a força com que a Terra atrai os corpos para o seu centro. Perto da superfície da Terra, o módulo desta força é: $$P = mg,$$ onde \(m\) é a massa do corpo e \(g\) (9,81 m/s²) é a constante conhecida como aceleração da gravidade.
- Força elástica \((\vec{F}_e)\)
- É a força que surge devido a deformação elástica dos corpos. (Ver seção Forças Elásticas )
- Força normal \((\vec{N})\)
- É a força que atua entre duas superfícies de contato. Sua direção é sempre ortogonal a superfície de contato. (Ver seção Força de Contato )

Na figura, o livro empura a mesa para baixo, por causa do seu peso, por reação, a mesa empurra o livro para cima. Esta força de reação é normalmente chamada de Força Normal. - Força de atrito \((\vec{F}_{at})\)
- É a força que atua entre duas superfícies de contato. Sua direção é sempre paralela a superfície de contato. Ela se opõe ao deslocamento das superfícies, uma em relação a outra. (Ver seção Força de Contato )

Na figura, a força que não deixa o bloco escorregar é a força de atrito que existe entre as duas superfícies. - Força de tração \((\vec{T})\)
- Chama-se força de tração a força que é exercida por uma corda ou haste.

A força que a corda faz no bloco pode ser chamada de força de tração. - Força Externa \((\vec{F}_{ext})\)
- São forças de agentes externos que não fazem parte do sistema de interesse. Em geral, as forças que não se encaixam nas definições acima são chamadas de forças externas, e tem origem diversas: motores, pessoas, animais e etc.
- Forças Internas \((\vec{F}_{int})\)
- São forças de componentes internos que fazem parte do sistema de interesse. Como elas formam um par ação-reação, não contribuem para a força resultante, pois anulam-se entre si.