O conceito de potencial elétrico está relacionado à medida da quantidade de energia potencial \((E_p)\) adquirida por uma carga unitária ao se deslocar em um campo elétrico. (Análogo ao potencial gravitacional, que se refere a energia do deslocamento de uma massa em um campo gravitacional.) Por definição, o potencial é uma grandeza escalar.

O potencial elétrico \(V_A\) no ponto \(A\) , é igual ao trabalho \(W_{A \rightharpoonup O}\) realizado pela força elétrica para levar uma unidade de carga do ponto \(A\) até o ponto \(O\) (origem do potencial). A posição do ponto \(O\) pode ser arbitrariamente escolhida, em geral, escolhemos a posição que facilite as contas dos problemas.

Para um conjunto finito de cargas, foi convencionado usar a origem do potencial, \(O\) , muito longe destas cargas (no infinito), \( O \rightarrow \infty\) . Matematicamente $$V_A = \frac{W_{A \rightharpoonup \infty}}{q},$$ isto é, o trabalho que é necessário para trazer uma carga \(q\) do infinito até o ponto \(A\) mais próximo das cargas geradoras do campo.

A unidade de potencial elétrico no S.I. é o Volt, \([V] = \frac{J}{C}\) (Joule por Coulomb).

Trabalho da força elétrica \((W_{A \rightharpoonup B})\) :

O trabalho resultante de uma carga elétrica \(q\) em um campo elétrico, que sofre um deslocamento do ponto \(A\) para o \(B\) , é dado por: $$ W_{A \rightharpoonup B} = q (V_B – V_A ),$$ onde \(V_A\) e \(V_B\) são os valores do potencial nos pontos \(A\) e \(B\) , respectivamente.

Energia potencial elétrica \((E_p)\) :

É a energia de uma carga \(q\) em um ponto \(A\) , na presença de um campo elétrico externo. Ou seja, é a energia do sistema formado pela carga e o campo externo onde ela se encontra imersa. Matematicamente: $$ E_p(A) = q V_A$$ onde \(V_A\) é o potencial no ponto \(A\) . A unidade de \(E_p\) é o joule \((J)\) .

Diferença de potencial:

A diferença de potencial, \(ddp\) , é igual ao trabalho por unidade de carga, que um agente externo deve realizar para deslocar uma carga \(q\) em um campo elétrico de \(A\) até \(B\) , sem alterar a energia cinética da carga. Ou seja, a diferença de potencial \(U\) entre os pontos \(A\) e \(B\) é $$U_{AB} \equiv V_B – V_A = \frac{W_{A \rightharpoonup B}}{q} = \frac{E_p(B) - E_p(A)}{q}.$$ Logo, a \(ddp\) também é a diferença de energia potencial elétrica (Joule) por unidade de carga elétrica (Coulomb).

Potencial devido a uma carga puntual:

O potencial de uma carga elétrica puntiforme \(q\) em um ponto \(A\) , em relação a um ponto de referência infinitamente afastado, é dado por: $$ V_A = k \frac{q}{d_A},$$ onde \(d_A\) é a menor distância da carga até o ponto \(A\) . Uma partícula de carga positiva produz um potencial elétrico positivo e uma negativa um potencial negativo.

Potencial elétrico devido a um conjunto de cargas puntuais:

O potencial devido a um conjunto de cargas puntiformes, num certo ponto do espaço, é igual a soma dos potenciais de cada carga.

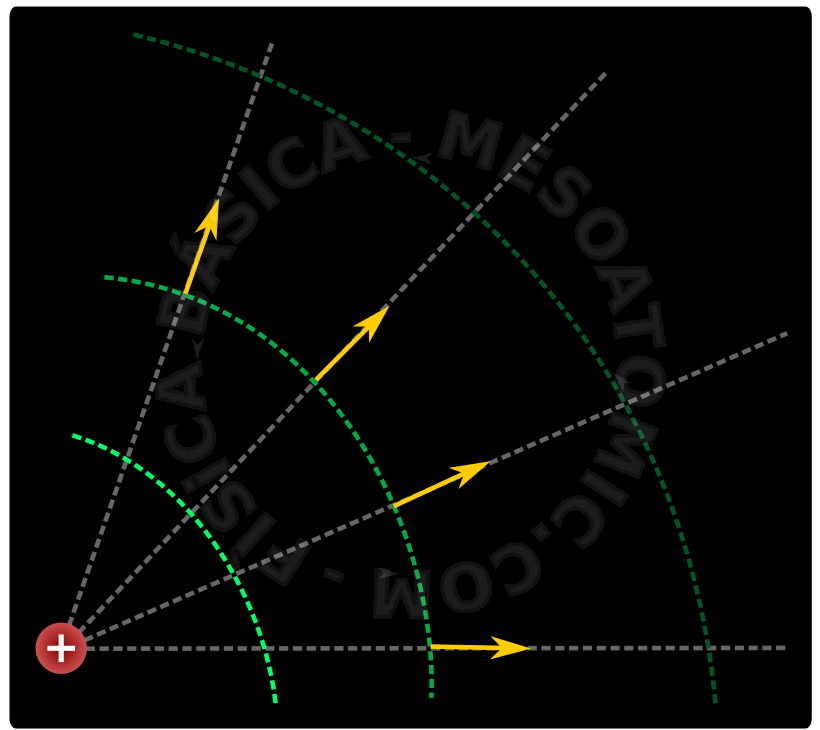
Linhas de campo:

As linhas de campo elétrico apontam no sentido do potencial decrescente.

Elétron-volt:

É uma unidade de energia comumente usada em física atômica e nuclear. É definida como a energia que um elétron ou próton adquire ao se mover através de uma diferença de potencial de \(1V\) , logo \(1eV=1,6 \times 10^{-19} J\) .

Superfícies equipotenciais

Superfícies equipotenciais são as regiões do espaço onde o potencial tem sempre o mesmo valor e apresentam as seguintes características:

• Os pontos sobre uma superfície equipotencial têm todos o mesmo valor de energia potencial;
• O trabalho realizado sobre uma carga de prova, para movê-la de uma determinada superfície para outra, é independente das localizações dos pontos inicial e final sobre elas e da trajetória que une os pontos;
• O campo elétrico é sempre perpendicular às superfícies equipotenciais.