- Óptica
- /
- Refracción, Lentes e Inst.
- /
- Refracción y medios refractivos
La velocidad de la luz cambia cuando se pasa de un medio a otro
Refracción
El fenómeno de refracción de la luz está asociada con el cambio de la velocidad de la luz al pasar de un medio a otro. La velocidad de la luz se modifica en la refracción, es decir, al pasar de un medio a otro.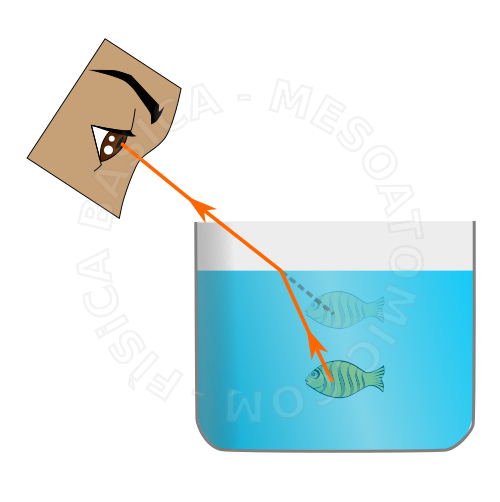
-
Para el estudio de la refracción, las siguientes definiciones son importantes:
- Dioptro
- Es el conjunto de dos medios separados por una superficie de refracción. Las sustancias que constituyen los medios de comunicación transparente se llaman medios refringentes. Cuanto mayor sea el refringencia de un medio menor será la velocidad de la luz en este medio.
- La velocidad de la luz en el vacío \((c)\)
- es de \(300.000 \frac{km}{s}\) o \(3.10^8 \frac{m}{s}\). La velocidad de la luz en el aire se aproxima al valor de velocidad en vacío.
- El índice de refracción absoluta \((n)\)
- Es la relación de la velocidad de la luz en el vacío, \(c\) , y la velocidad de la luz en el medio en cuestión:
- \begin{equation} n=\frac{\text{velocidad de la luz en el vacio}}{\text{velocidad de la luz en el medio}} = \frac{c}{v}. \end{equation} Ejemplos de materiales con diferentes índices de refracción:
-
Sustancia \(n\) Agua pura 1.33 Sal de mesa 1.54 Diamante 2.42 Alcohol etílico 1.36 Glicerina 1.47 Corona cristal 1.52 Hielo 1.31 Parafina 1.43 - El índice de refracción relativo
- de un medio \(A\) en relación uno con otro a través de \(B\) se obtiene de la fórmula: \begin{equation} n_{ab}=\frac{n_{A}}{n_{B}}=\frac{v_{B}}{v_{A}}, \end{equation} donde \(n_A\) es el índice de refracción del medio \(A\) y \(n_B\) es el índice de refracción del medio \(B\) .
Leyes de refracción
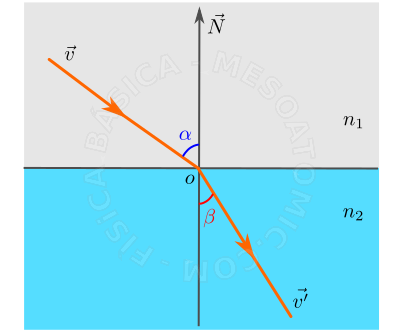
Para un rayo de luz incidente sobre la interface de dos medios con diferentes índices de refracción, el rayo incidente y el refractado no estarán en el mismo plano. Los ángulos que estos rayos hacen con el vector normal de la interfaz entre los medios se pueden encontrar con la ley de Snell-Descartes, que dice: Para un haz monocromático de luz que pasa de un medio para otro, el producto del sino del ángulo, formado por el rayo y la normal, con al índice de refracción del medio en el que este rayo se encuntra es constante. Matemáticamente, tenemos \begin{equation} n_{1} sen(\alpha) =n_{2} sen(\beta). \end{equation} Obsérvese que cuando el haz de luz pasa de un medio menos refrigente(mayor velocidad) para un medio más refrigente(menor velocidad) este se aproxima a la normal, y viceversa. La figura a continuación ilustra este fenómeno.
Reflexión total
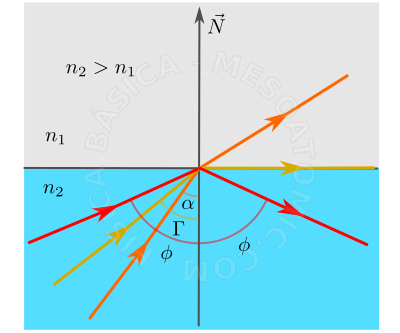
Cuando la luz pasa desde un medio más refringente para un menos refringente, existe un ángulo límite, de manera que para ángulos mayores de este, el haz de luz no puede cambiar de medio, de modo que el haz se refleja totalmente en la interfaz de los medios. Este fenómeno es importante para aplicaciones tales como la fibra óptica y telescopios. El ángulo límite \(\Gamma\) se define como el ángulo incidente que corresponde a una, emergencia rasante de \(90^{o}\) cuando la luz se propaga desde el medio más de refracción para los menos de refracción medio, es decir, \begin{equation} sen(\Gamma)=\frac{n_{1}}{n_{2}}\text{, para }n_{1} \lt n_{2}. \end{equation}
Dioptro plano
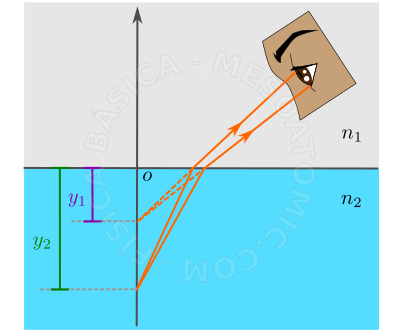
Láminas de caras paralelas
Cuando un haz de luz atraviesa una lámina de cara paralela, el sale de un medio con un índice de refracción dado, digamos \(n_1\), pasa a través de un medio con índice \(n_2\), y vuelve al medio de refracción \(n_1\) . Usando las leyes de la refracción, nos encontramos con que el haz que emerge en medio de refracción \(n_2\) será paralela al haz incidente en este medio, véase el gráfico a continuación.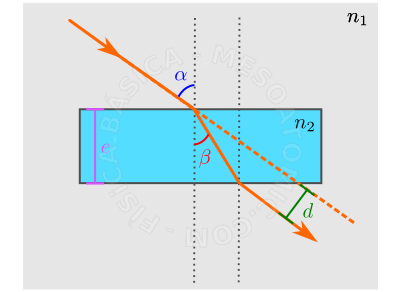
Prisma
El sistema óptico constituido por tres medios homogéneos y transparentes separados por dos superficies planas no paralelas se denomina prisma.
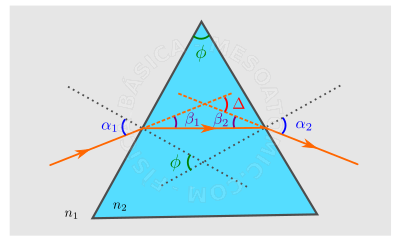
Ver la figura anterior. Para este sistema podemos relacionar el ángulo entre las dos caras del prisma, \(\phi\) , con los ángulos de las normales internas \(\beta_1\) y \(\beta_2\) : \begin{equation} \phi = \beta_1 + \beta_2. \end{equation} También es posible encontrar el ángulo que el rayo incidente en el prisma hará con el rayo que emerge del prisma, \(\Delta\) , es decir, \begin{equation} \Delta = \alpha_1 + \alpha_2 - \phi, \end{equation} donde \(\alpha_1\) y \(\alpha_2\) son los ángulos que el rayo de luz forma con la normal a la luz externa.
El análisis de prismas ópticos revela que la desviación asume el valor mínimo, \(\Delta_{min}\) cuando el ángulo de incidencia en \(1^a\) cara y de emergencia en \(2^a\) cara fueran iguales ( \(\alpha_1 = \alpha_2\) ) tal que: \begin{equation} \Delta_{min} = 2 \alpha_{1} - \phi. \end{equation}